Trabajo Práctico 1 y 2 de Matemática

 

1. Números Reales: El término proviene del latín numerus y hace referencia a un signo o un conjunto de signos. La teoría de los números agrupa a estos signos en distintos grupos.Los números reales son los que pueden ser expresados por un número entero (3, 28, 1568) o decimal (4,28; 289,6; 39985,4671). Esto quiere decir que abarcan a los números racionales (que pueden representarse como el cociente de dos enteros con denominador distinto a cero). Los números reales se clasifican en números racionales e irracionales. En el primer grupo se encuentran a su vez dos categorías: los enteros, que se dividen en tres grupos (naturales, 0, enteros negativos).
2. Conjunto de números (reales, enteros, racionales, naturales, irracionales)
3. Números naturales N: Los números naturales son los que desde el principio de los tiempos se han utilizado para contar. se denota como N y se representan así N= {1,2,3,4,5,6…}Cuando restamos o dividimos dos números naturales, el resultado no es necesariamente un número natural, y por eso decimos que los números naturales no son cerrados respecto estas dos operaciones. En cambio, sí son cerrados respecto a la suma y la multiplicación, es decir, la suma o multiplicación de dos números naturales da siempre como resultado otro número natural.
4. Números enteros Z: Cuando aparece la necesidad de distinguir unos valores de otros a partir de una posición de referencia es cuando aparecen los números negativos. Por ejemplo, cuando desde el nivel 0 (nivel del mar) queremos diferenciar por encima del nivel del mar o por debajo del mar (en las profundidades). Al conjunto formado por los enteros negativos, el número cero y los enteros positivos (o naturales) lo llamamos conjunto de los números enteros. Se denota con el símbolo Z  y se pueden escribir como Z= {..., -3, -2, -1, 0, 1, 2, 3…}Los representamos en una recta numérica de la siguiente manera:
5. Números racionales Q: Los números racionales son los números que resultan de la razón (división) entre dos números enteros. Se denota el conjunto de los números racionales como,Q así que Q= {p_q|p, q E Z }
6. Luego en el segundo trabajo tuvimos esta actividad;  Que en Geometría y Álgebra elemental, una función lineal es una función polinómica de primer grado; es decir, una función cuya representación en el plano cartesiano es una linea recta. Esta función se puede escribir como: F= (MX + B) donde M y B son constantes reales, M, B, L, €, ℝ y )( es una variable real. La constante M es la pendiente de la recta. Y B es el punto de corte de la recta con el eje Y. Si se modifica M entonces se modifica la inclinación de la recta, y  si se modifica B, entonces la linea se desplazara hacia arriba o hacia abajo.       Un Ejemplo: 6x + 2 :El dominio y la imagen en esta función son los números reales. 
7. Llamamos función cuadrática a las funciones polinómicas de dos grados; cada punto tiene 2 componentes X la llamamos absiza y Y ordenada. La imagen de la función cuadrática son de los valores de la variable Y...  Un Ejemplo: (Yv; + ∞)Gráfica hacia arriba.                     (Yv; - ∞ ) Gráfica hacia abajo. 
8. En el Trabajo Práctico de Funciones, tenemos un ejercicio que trata de:
   
9. a) 10 afectan el primer día                        b) En el 2 día fue 15 afectados              b)La función representada  
10. 

¿QUÉ ES LA TRIGONOMETRÍA? 

La palabra trigonometría es un sustantivo que deriva de dos raíces griegas: por una parte τριγωνο (trigoño= tres ángulos) o sea para nosotros "triangulo" y μετρον (metron) para nosotros "medida".

Es el estudio de las relaciones existentes entre todas las medidas (de lados y ángulos) de un triángulo. Cabe señalar, no obstante que el enfoque meramente triangular de trigonométrica es antiguo.

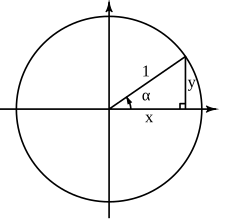
La circunferencia trigonométrica o unitaria esta dicha función es una circunferencia de RADIO uno, normalmente con su centro en el origen (0. 0) de un sistema de coordenadas, de un plano complejo. 

Se utiliza con el fin de poder estudiar fácilmente las razones trigonométricas y función trigonométrica, mediante la representación de triángulos rectángulos auxiliares. 

Por ejemplo, en el primer ejercicio tenemos que indicar en que cuadrante pertenecen los ángulos en la circunferencia:

a) 300° b) -200° c) 760° d)160° 

El primer ángulo pertenece al IV cuadrante, porque la circunferencia es positivo gira a la izquierda y en negativo a la derecha, en los cuatro cuadrantes hay diferentes ángulos , en este primer caso el IV cuadrante tiene 270° - 360° por lo tanto es ahí donde pertenece el angulo 300°.

El segundo caso pertenece  al III cuadrante porque ahí se encuentra los ángulos de 180° - 270°.

En el tercer caso pertenece al I cuadrante por ser uno de los menores números de ahí que son de 0° - 90°.

El cuarto caso pertenece al II cuadrante porque sus ángulos son de 90° - 180°. 

Otro ejemplo serían Los números opuestos.

"El ángulo opuesto de a es -a"

Si a esta en el I cuadrante -a se encuentra en el IV cuadrante, porque al ser opuestos se encuentran debajo del otro. Como cuando a se encuentra en el II cuadrante del -a pertenecería al III cuadrante.